4.2 MIT and Harvard

The late 1950s and the decade of the 1960s saw significant development in computer graphics-related computing, displays, and input and output hardware. The nature of the computer at this point in history was that it allowed programs to be written to accomplish different functions. But in the early days of computer graphics, users purchased their hardware, and the burden of developing these reusable programs, often including the development of the underlying algorithms for creating images, fell on the shoulders of the individual user.

Researchers at universities and laboratories around the world began to investigate techniques that could harness the power of the computer and its display and interaction devices to solve problems and provide capabilities that may have been outside of the reach of certain users because of the complexity of this programming process. A software industry was spawned, and turnkey systems were marketed that buffered the individual user from the computer instructions necessary to use the system to its potential.

 MIT

Some of the early work in computer graphics related algorithm and software development took place at the Massachusetts Institute of Technology, and at Harvard University just up the Charles River.

Tom Stockham was at Lincoln Labs on a project to use computers to process photographic material. His technique was to use a facsimile machine to “digitize” a photograph so that each element of the picture (what would later come to be known as the pixel) could be represented as a number in memory that represented a shade of gray. Once he had this image in digital form, he manipulated properties such as dynamic range and contrast, and then re-photographed the image from the screen of a CRT. Hence, what is now common in software packages such as Photoshop, that is, image processing, was developed.

A professor in the Mechanical Engineering Department at MIT during the 1950s and 1960s, Steven Coons, had a vision of interactive computer graphics as a powerful design tool. During World War II, he worked on the design of aircraft surfaces, developing the mathematics to describe generalized “surface patches.” At MIT’s Electronic Systems Laboratory he investigated the mathematical formulation for these patches, and in 1967 published one of the most significant contributions to the area of geometric design, a treatise which has become known as “The Little Red Book”.

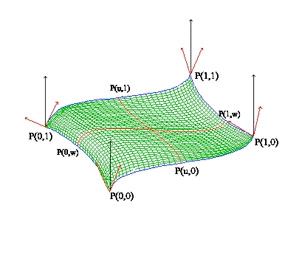
His “Coons Patch” was a formulation that presented the notation, mathematical foundation, and intuitive interpretation of an idea that would ultimately become the foundation for surface descriptions that are commonly used, such as b-spline surfaces, NURB surfaces, etc. His technique for describing a surface was to construct it out of collections of adjacent patches, which had continuity constraints that would allow surfaces to have curvature which was expected by the designer. Each patch was defined by four boundary curves, and a set of “blending functions” that defined how the interior was constructed out of interpolated values of the boundaries.

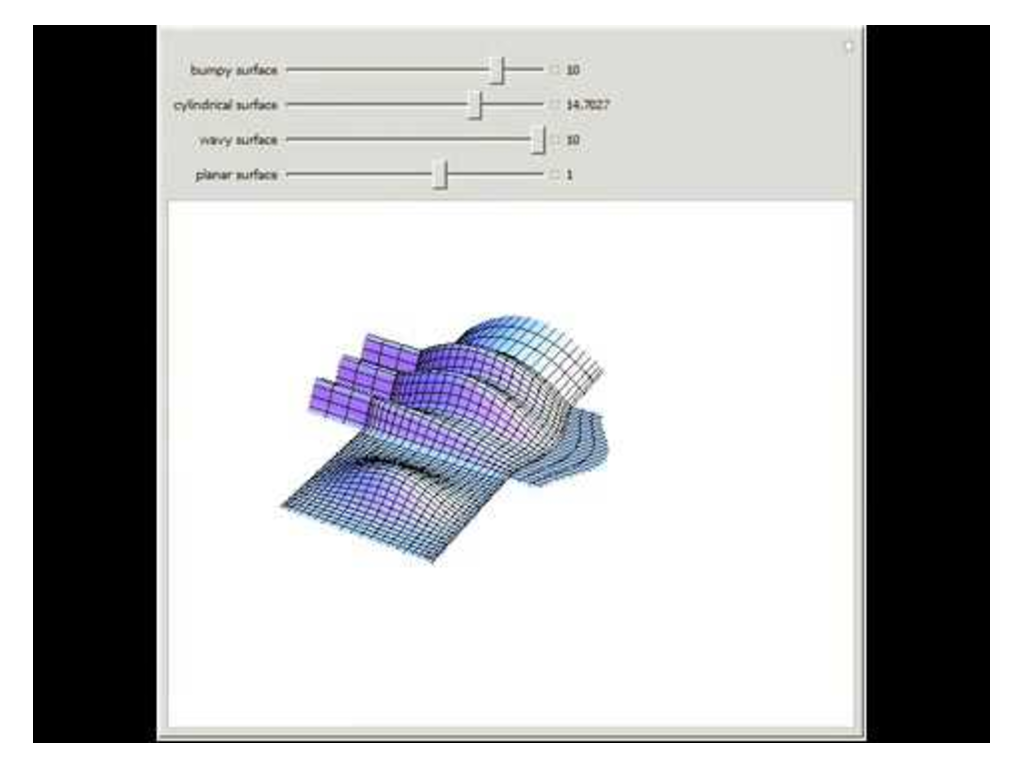
Movie 4.1 – Generalized Coons Surface, From Wolfram’s Mathematica demonstration

Two of Coons’ students were Ivan Sutherland and Lawrence Roberts, both of whom went on to make numerous contributions to computer graphics and (in Roberts’ case) to computer networks.

Lawrence Roberts wrote the first algorithm to eliminate hidden or obscured surfaces from a perspective picture. In 1965, Roberts implemented a homogeneous coordinate scheme for transformations and perspective. His solutions to these problems prompted attempts over the next decade to find faster algorithms for generating hidden surfaces, many of which were investigated at the University of Utah (Section 3 in this chapter).

Harvard University

After leaving MIT, Ivan Sutherland went briefly to ARPA, and was then recruited by Harvard. There he engaged in studies to produce pictures with dynamic perspective. The following account of these research activities at Harvard is from FUNDING  A REVOLUTION : Government Support for Computing Research, published by the National Research Council in 1999.

In 1966, Ivan Sutherland moved from ARPA to Harvard University as an associate professor in applied mathematics. At ARPA, Sutherland had helped implement J.C.R. Licklider’s vision of human-computer interaction, and he returned to academe to pursue his own efforts to extend human capabilities. Sutherland and a student, Robert Sproull, turned the “remote reality” vision systems of the Bell Helicopter project into VR by replacing the camera with computer-generated images. The first such computer environment was no more than a wire-frame room with the cardinal directions–north, south, east, and west–initialed on the walls. The viewer could “enter” the room by way of the “west” door and turn to look out windows in the other three directions. What was then called the head-mounted display later became known as VR.

Sutherland’s experiments built on the network of personal and professional contacts he had developed at MIT and ARPA. Funding for Sutherland’s project came from a variety of military, academic, and industry sources. The Central Intelligence Agency provided $80,000, and additional funding was provided by ARPA, the Office of Naval Research, and Bell Laboratories. Equipment was provided by Bell Helicopter. A PDP-1 computer was provided by the Air Force and an ultrasonic head-position acoustic sensor was provided by MIT Lincoln Laboratory, also under an ARPA contract.

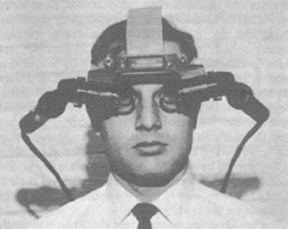
Sutherland outlined a number of forms of interactive graphics that later became popular, including augmented reality, in which synthetic, computer-generated images are superimposed on a realistic image of a scene. He used this form of VR in attempting a practical medical application of the head-mounted display. The first published research project deploying the 3D display addressed problems of representing hemodynamic flow in models of prosthetic heart valves. The idea was to generate the results of calculations involving physical laws of fluid mechanics and a variety of numerical analysis techniques to generate a synthetic object that one could walk toward and move into or around (Greenfield et al., 1971).

As Sutherland later recalled, there was clearly no chance of immediately realizing his initial vision for the head-mounted display. Still, he viewed the project as an important “attention focuser” that “defined a set of problems that motivated people for a number of years.” Even though VR was impossible at the time, it provided “a reason to go forward and push the technology as hard as you could. Spin-offs from that kind of pursuit are its greatest value.”

Several of the original Harvard group also helped form [Evans and Sutherland], including Charles Seitz, who joined the Utah faculty in 1970 and remained until 1973, when he moved to California Institute of Technology and founded Myricom with Dan Cohen, another Harvard alumnus who contributed to the head-mounted display. The interaction between research on basic problems and development of hardware and software for military projects at Evans & Sutherland was an important feature of work at [the University of] Utah.

Sutherland’s group also developed the first clipping algorithm, eliminating any part of a synthetic environment that was outside the “camera’s” field of view, making it less computationally intensive to generate a scene on the screen.

William Newman was also at Harvard during this period. He was interested in the construction of command languages for interactive computer use. His ideas on command language programming have been very important in the evolution of the human-computer graphical interface. Newman was co-author with Robert Sproull of Carnegie Mellon of one of the most influential textbooks in the area of computer graphics, Principles of Interactive Computer Graphics, published by McGraw-Hill in 1973. Newman went on to continue his HCI work at Xerox PARC.