19.6 Plants

Dr. Przemyslaw Prusinkiewicz‘s interest in computer graphics began in the late 1970s. By 1986 he originated a method for visualizing the structure and growth of plants based on L-systems, a mathematical theory of development of multicellular organisms introduced by the late Professor Aristid Lindenmayer. Prusinkiewicz, his students, and collaborators transformed L-systems into a powerful programming language for expressing plant models, and extended the range of phenomena that can be simulated. Specifically, parametric L-systems facilitate the construction of models by assigning attributes to their components. Differential L-systems make it possible to simulate plant growth in continuous time, which is essential to the animation of developmental processes. Environmentally-sensitive and open L-systems provide a framework for simulating the interactions between plants and their environment. The power of these concepts is demonstrated by the wide range of biological structures already modeled, from algae to wild flowers to gardens and stands of trees competing for light.

In addition to the important extensions of L-systems, Prusinkiewicz’s research also includes studies of fundamental problems of morphogenesis – emergence of patterns and three dimensional forms in nature. This includes the modeling of spiral phyllotactic patterns in plants, and developmental patterns and forms of seashells.

As a result of the research on the extension of L-systems, plants can be modeled with unprecedented visual and behavioral fidelity to nature. Prusinkiewicz authored the book, The Algorithmic Beauty of Plants, demonstrating that plant models can be combined artistically into stunning and inspiring images. His website, Visual Models of Morphogenesis: A Guided Tour is a spectacular explanation of the techniques used to model organic shapes such as plants.

The website for Prusinkiewicz’ research lab at the University of Calgary can be found at

http://www.cpsc.ucalgary.ca/Research/bmv/vmm-deluxe/TableOfContents.html

John Hutchinson demonstrated in 1981 a branch of mathematics now known as Iterated Function Theory. Later in the decade Michael Barnsley, a leading researcher from Georgia Tech, wrote the popular book Fractals Everywhere. The book presented the mathematics of Iterated Functions Systems (IFS), and proved a result known as the Collage Theorem.

An IFS fractal, according to Barnsley, is defined by a set of elementary geometric transformations which are called “linear” or “affine” by mathematicians. In the everyday language, they are a combination of

• translations
• rotations
• linear compressions along the vertical or horizontal axis, or both. The compression ratios along the two axes can be different.
• vertical or horizontal shears, such that a rectangle is transformed into a parallelogram through the sliding of a side along itself.

The only requirement is that the transformations must be contractive, i.e. the distance between two points must decrease (at least, not increase) in the transformation.The transformations to be implemented in the IFS set depend upon the figure to be redrawn. As Barnsley stated, “There is a magical precept that must be satisfied: if the target figure is transformed through the various transformations in the set, one must get exact parts of this figure, and superimposing all these parts must reconstruct the whole figure.”

The Collage Theorem presented a possibility that intrigued researchers, particularly Barnsley and some of his students. If, in the forward direction, fractal mathematics is good for generating natural looking images, then, in the reverse direction, could it not serve to compress images? Going from a given image to an Iterated Function System that can generate the original (or at least closely resemble it), is known as the inverse problem.

Barnsley and his research team applied the Collage Theorem to try and solve the inverse problem, and published the technique in articles for Computer Graphics World and a famous article in the January 1988 Byte Magazine issue. He and Alan Sloan applied for and were granted a software patent, and left Georgia Tech to found Iterated Systems Inc. This Byte article didn’t really address the inverse problem directly, but it did exhibit several images purportedly compressed in excess of 10,000:1.

The images were given suggestive names such as “Black Forest” and “Monterey Coast” and “Bolivian Girl” and they were all manually constructed.

Midori Kitagawa, an associate professor in the Department of Art and the Advanced Computing Center for the Arts and Design at Ohio State, developed the Branching Object Generation and Animation System (BOGAS) ^[1] to create realistic models of trees, plants, blood vessels, nervous systems, underwater animals and even imaginary creatures. The system was designed to help scientists, botanists and artists visualize realistic branching objects, permitting them to generate the objects interactively and then to see how factors like gravity and sunlight affect growth.

Movie 19.18 I Have Never Seen, But I Know…

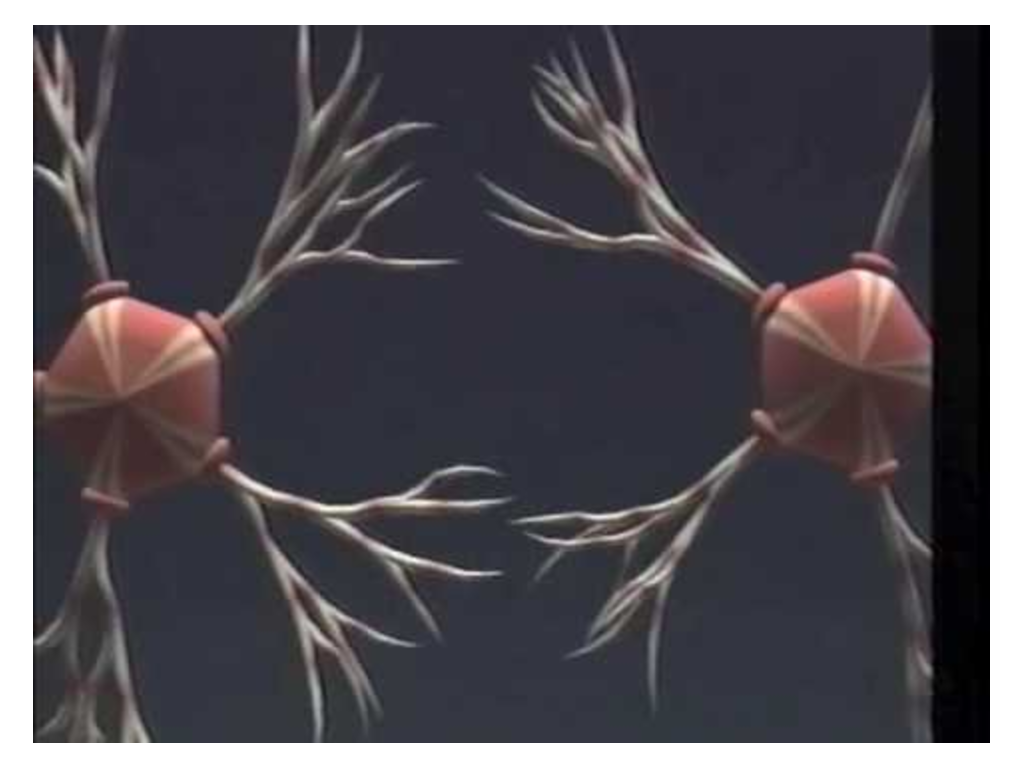
https://www.youtube.com/watch?v=Xb50LQ8lhAU
Film by Midori Kitagawa (1990) using the BOGAS system for plant generation. Music by Daniel Remler (Ohio State University ACCAD)

Gallery 19.4 Images from Prusinkiewicz